先来一段来自百度百科的介绍

树状数组(Binary Indexed Tree(B.I.T), Fenwick Tree)是一个查询和修改复杂度都为log(n)的数据结构。主要用于查询任意两位之间的所有元素之和，但是每次只能修改一个元素的值；经过简单修改可以在log(n)的复杂度下进行范围修改，但是这时只能查询其中一个元素的值(如果加入多个辅助数组则可以实现区间修改与区间查询)。 简单的说，它是一种树形数据结构，可以快速查询和修改值。 大概长这样子

树状数组
树状数组

常用的场景

如果给你n个数，然后进行q次询问，每次询问一个区间[x,y]的和，相信很多人都会用前缀和数组：sum[i]=a[1]+a[2]+…+a[i]，复杂度O(n)。但是如果再进行q次的单点更改，前缀和数组就派不上用场了。这时候可以考虑用树状数组降低复杂度。

具体实现

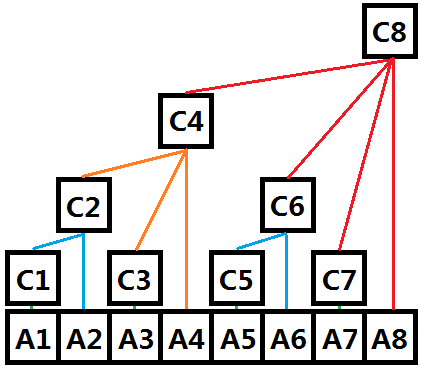
从上面的图可以知道，a[i]代表原数组的值，c[i]代表树状数组（采用下标模拟树形结构）,c[i]表示a数组前i项和。

然后有：

1
2
3
4
5
C[1] = A[1]
C[2] = A[1] + A[2]
C[3] = A[3]
C[4] = C[2]+C[3]+A[4] = A[1]+A[2]+A[3]+A[4]
...

按上图，现在如果我要查询前4项的和，有

1
sum[4] = C[4] (100)

如果我要查询前6项的和，有

1
sum[6] = C[6]+C[4] (110 + 100)

如果我要查询前7项的和，有

1
sum[7] = C[7]+C[6]+C[4] (111 + 110 + 100)

上面右侧括号里的是C数组下标二进制表示，因此，有大牛总结出了规律

对于sum[7]来说，它对应的C数组下标为当前下标减去最后一个二进制1，直到为0。是这样的，7（111），最后一个二进制1在第一位，减去第一位的1变成6（110），以此类推4（100），0（000）。

对于如何求一个二进制最后一位1，有人给出了一个公式，具体证明可查阅相关资料 \[ lowbit(x)=x\&(−x) \] 因此，如果想要求前x项和，只需要一个循环即可

1
for (int i = x; i > 0; i -= lowbit(i));

如果想要更改某一点的值，不仅仅只更改一处，还要向上更改，例如更改上图的C[3]，与C[3]有关系的点还有C[4], C[8]。

因为更改和查询互为逆过程，因此每次将当前坐标加上当前坐标最后一位1

1
for (int i = x; i <= n; i += lowbit(i));

总结

总结一下，树状数组有三个重要函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
// 获取x最后一个二进制1
inline int lowbit(int x) {
    return x & (-x);
}

// 修改某一处的值
inline void add(int x, int val) {
    for (int i = x; i <= n; i += lowbit(i))
        c[i] += val;
}

// 查询前x项和
inline int sum(int x) {
    int ans = 0;
    for (int i = x; i; i -= lowbit(i))
        ans += c[i];
    return ans;
}

可以做做poj2352题目练习一下